Volver a Guía
Ir al curso
CURSO RELACIONADO
Matemática 51
2025
GUTIERREZ (ÚNICA)
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
MATEMÁTICA 51 CBC
CÁTEDRA GUTIERREZ (ÚNICA)
14.
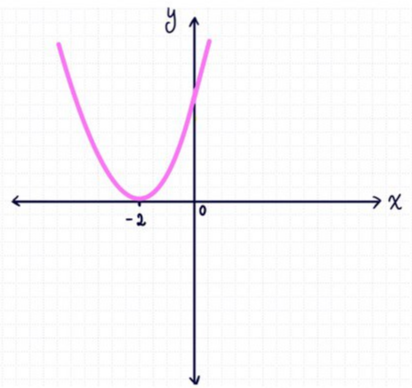
Hallar el vértice de la parábola que es el gráfico de la función $f$. Dar la imagen y los intervalos de crecimiento y de decrecimiento de $f$. Graficar $f$.
b) $f(x) = (x+2)^2$
b) $f(x) = (x+2)^2$
Respuesta
Identifiquemos primero qué tipo de estructura de función cuadrática tenemos (polinómica, factorizada o canónica).
Es canónica: $f(x) = a(x-Xv)^2 + Yv$, donde $a = 1$, $Xv = -2$ e $Yv = 0$
El vértice de la función se encuentra en el punto $(Xv, Yv)$, el cual sale de la estructura de la función, ya que $Xv = -2$ e $Yv = 0$.
$V = (-2,0)$
La imagen de la función depende del signo de $a$ y del valor de $Yv$. Como $a>0$ la imagen tendrá la forma $[Yv, +\infty)$.
$\text{Im}f = [0, +\infty)$
Los intervalos de crecimiento y de decrecimiento dependen del signo de $a$ y del valor de $Xv$. Como $a>0$ los intervalos tendrán la forma $I\uparrow = (Xv, +\infty)$ e $I\downarrow =(-\infty, Xv)$
Reportar problema
$I \uparrow = (-2, +\infty)$
$I \downarrow = (-\infty, -2)$

🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
